Optimization Problems and Applications
Acknowledgment
This document is based on the lecture videos by Dr. Emre Sefer, originally delivered as part of the course Machine Learning in Finance at Ozyegin University. The lecture videos can be accessed at the following link: Dr. Emre Sefer’s Lecture Videos.
The content has been compiled and published by FinanceLab.AI. For more information, visit our website: FinanceLab.AI.
Additionally, the material draws on concepts from:
-
Boyd, Stephen P., and Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004. ISBN: 9780521833783.
General Optimization Problem
The general optimization problem is expressed in the standard form as follows:
| Minimize: | f0(x) | ||
| Subject to: | fi(x) ≤ 0, i = 1,…,m, | ||
| hi(x) = 0, i = 1,…,p, |
where:
-
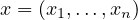 is the vector of optimization variables,
is the vector of optimization variables,
-
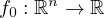 is the objective function we aim to minimize,
is the objective function we aim to minimize,
-
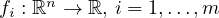 , are the inequality constraint functions that
ensure
, are the inequality constraint functions that
ensure 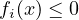 ,
,
-
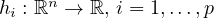 , are the equality constraint functions that
ensure
, are the equality constraint functions that
ensure 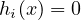 .
.
The goal is to find an optimal solution 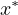 that minimizes
that minimizes 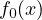 while
satisfying all the constraints.
while
satisfying all the constraints.
Key Characteristics of the Problem
The functions 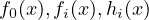 map an
map an 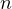 -dimensional vector
-dimensional vector 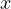 (the input
variables) to a scalar value. This mapping is represented as
(the input
variables) to a scalar value. This mapping is represented as 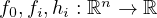 .
.
-
For inequality constraints,
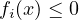 must hold for
must hold for 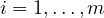 .
.
-
For equality constraints,
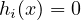 must hold for
must hold for 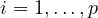 .
.
This general formulation covers various types of optimization problems,
and the solution depends on the specific properties of 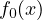 ,
, 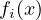 , and
, and
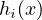 .
.
Convex vs Non-Convex Optimization
If the objective function 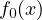 and all constraint functions are convex, the problem
is called a convex optimization problem. Convex optimization guarantees that
the solution
and all constraint functions are convex, the problem
is called a convex optimization problem. Convex optimization guarantees that
the solution 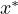 is a global optimal solution.
is a global optimal solution.
However, in non-convex optimization problems, the functions may contain
multiple local minima. As a result, the solution 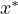 may only be a local optimum,
meaning it is not necessarily the best solution globally.
may only be a local optimum,
meaning it is not necessarily the best solution globally.
Applications of Optimization
Optimization is a fundamental tool used in various fields, including electrical engineering, financial engineering, machine learning, and biomedical applications. Below are some examples:
Electrical Engineering Applications
-
Circuit Design: Optimization is used to size devices (e.g., transistors) to minimize power consumption while adhering to manufacturing constraints, timing requirements, and area limitations.
-
Signal Processing: Problems like filter design are formulated as optimization tasks to achieve the desired signal characteristics.
-
Communication Systems: Optimization helps in designing transceivers, beamforming, and power control to minimize interference and maximize efficiency.
Financial Engineering Applications
-
Portfolio Optimization: The objective is to allocate investments across assets to maximize returns and minimize risks (variance). Constraints include budget limits, minimum returns, and maximum investment per asset.
-
Index Tracking: Instead of buying all constituents of an index (e.g., S&P 500), optimization is used to select a subset of assets that replicate the index’s performance.
Example: Portfolio Optimization
In portfolio optimization, we allocate investments among different assets such as stocks, bonds, or treasury bills. For example:
-
Let Apple stock account for 40% of the portfolio,
-
Microsoft stock account for 30%,
-
A three-month treasury bill account for 30%.
The goal is to minimize the overall risk (variance) of the portfolio while meeting constraints such as minimum return requirements, budget limits, and diversification constraints.
Example: Power Control in Wireless Networks
The signal-to-interference-plus-noise ratio (SINR) at the 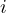 -th receiver is
given by:
-th receiver is
given by:
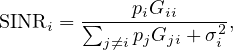
where:
-
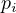 is the power used by the
is the power used by the 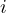 -th transmitter,
-th transmitter,
-
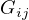 is the path gain from transmitter
is the path gain from transmitter 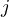 to receiver
to receiver 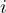 ,
,
-
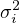 is the noise power at the
is the noise power at the 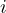 -th receiver.
-th receiver.
The problem is to maximize the weakest SINR (minimum SINR across all receivers), subject to power constraints:
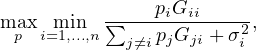
subject to:
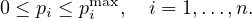
This problem is typically non-convex, meaning that the solution found may only be a local optimum and is not guaranteed to be the global optimal solution.
Optimization in Machine Learning
Many problems in machine learning are formulated as optimization tasks. Examples include:
-
Training neural networks involves minimizing a loss function that represents the error between predictions and true values.
-
Support vector machines optimize a margin to separate data points belonging to different classes.
-
Clustering algorithms, such as
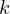 -means, optimize the allocation of data
points to clusters to minimize intra-cluster distances.
-means, optimize the allocation of data
points to clusters to minimize intra-cluster distances.
Formulating Optimization Problems
An optimization problem has three main components:
-
Variables: Unknowns to be optimized, e.g., power levels or asset allocations.
-
Constraints: Represent limitations, such as
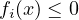 (inequality) and
(inequality) and
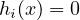 (equality).
(equality).
-
Objective: The function
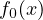 to be minimized or maximized.
to be minimized or maximized.
For example, in electronic circuit design, the variables may represent device widths and lengths, the constraints may include manufacturing limits and timing requirements, and the objective may be minimizing power consumption.
Conclusion
Optimization plays a crucial role in various domains. From minimizing risks in financial portfolios to improving power efficiency in circuits and wireless networks, its applications are vast. While convex optimization guarantees global solutions, non-convex problems remain challenging, requiring advanced techniques for satisfactory results.
References
This document draws on material from the following sources:
-
Dr. Emre Sefer’s lecture videos, which can be accessed at: Dr. Emre Sefer’s Lecture Videos, and published by FinanceLab.AI (FinanceLab.AI).
-
Boyd, Stephen P., and Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004. ISBN: 9780521833783.